Operaciones con triángulos

Un tri·ngulo es un polÌgono de tres lados, y por lo tanto tres vÈrtices. Se cumple que la suma de los ·ngulos de un tri·ngulo es siempre 180∫.

CLASIFICACI”N DE TRI¡NGULOS SEG⁄N SUS LADOS.

Bas·ndonos en la medida de sus lados podemos clasificar los tri·ngulos en tres tipos:

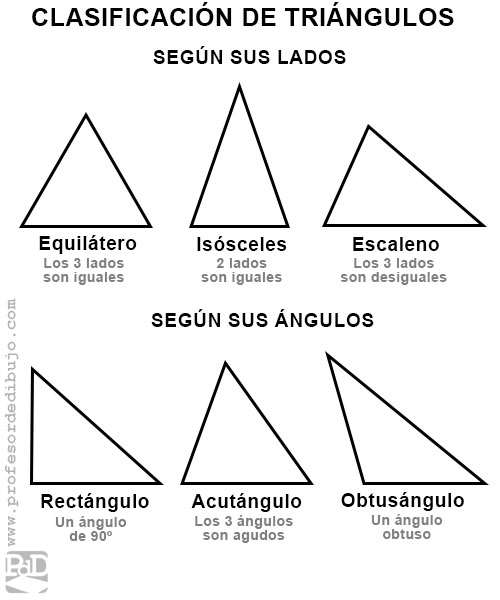
• Equil·teros: son tri·ngulos que tienen todos sus lados iguales.
• IsÛsceles: son tri·ngulos que tienen dos de sus lados iguales.
• Escalenos: son tri·ngulos que tienen todos sus lados desiguales.
  
  

CLASIFICACI”N DE TRI¡NGULOS SEG⁄N SUS ¡NGULOS.

Seg˙n la amplitud de sus ·ngulos, podemos clasificar los tri·ngulos de la siguiente manera:

• Rect·ngulos: son tri·ngulos que tienen un ·ngulo recto (90∫). El lado opuesto al ·ngulo recto se denomina hipotenusa y los otros dos son los catetos.
• Acut·ngulos: son tri·ngulos que tienen los tres ·ngulos agudos (miden menos de 90∫).
  
  
• Obtus·ngulos: son tri·ngulos que tienen un ·ngulo obtuso (mayor de 90∫).

 

CONSTRUCCION DE TRIANGULOS

1.- ConstrucciÛn de un tri·ngulo equil·tero a partir del lado

2.- ConstrucciÛn de un tri·ngulo equil·tero inscrito en una circunferencia

3.- ConstrucciÛn de un tri·ngulo conocidos sus tres lados

4.- ConstrucciÛn de un tri·ngulo conocido un lado "a" y sus ·ngulos adyacentes "B" y "C"

5.- ConstrucciÛn de un tri·ngulo conocidos dos lados "a" y "b" y el ·ngulo entre ellos "C"

6.- ConstrucciÛn de un tri·ngulo conociendo el lado "a", un ·ngulo adyacente "B" y el  lado opuesto "b".

7.- ConstrucciÛn de un tri·ngulo, conociendo el lado "a", la altura de "A" y el ·ngulo "B"

8.- ConstrucciÛn de un tri·ngulo conociendo el lado "a", la altura de "A" y el lado "b"

9.- ConstrucciÛn de un tri·ngulo, conociendo el lado "a", el ·ngulo opuesto "A" y el lado "b"

10.- ConstrucciÛn de un tri·ngulo, conociendo el lado "a", el ·ngulo opuesto "A" y la altura de "A"

11.- ConstrucciÛn de un tri·ngulo, conociendo el lado "a", un ·ngulo adyacente y el ·ngulo opuesto "A"

PUNTOS NOTABLES DEL TRIANGULO

1.- Ortocentro. (Alturas del tri·ngulo)

El ortocentro sirve para determinar la naturaleza de un triangulo cuando no se conocen las medidas de sus lados:

• Si el ortocentro es un punto interior, entonces el triangulo es ACUTANGULO
• Si el ortocentro coincide con uno de los vertices, entonces el triangulo es RECTANGULO y el vÈrtice es el angulo de 90∫
• Si el ortocentro es un punto externo, entonces el triangulo es OBTUSANGULO

2.- Baricentro. (Medianas)

El Baricentro se utiliza para determinar el centro de gravedad del tri·ngulo

3.- Incentro. (Bisectrices)

El Incentro se utiliza para determinar el centro de la circunferencia inscrita en un tri·ngulo

4.- Circuncentro. (Mediatrices)

El Circuncentro se utiliza para determinar el centro de la circunferencia en la cual est· inscrito un tri·ngulo

---

Ejercicios